Alguns padrões e estratégias para resolver problemas matemáticos
Originalmente eu havia postado esse conteúdo aqui:
Existem algumas estratégias de natureza heurística usadas para abordar
vários tipos de problemas como, por exemplo, considerar os pontos extremos de
alguma coisa, procurar os "invariantes", ou seja, aquilo que não muda
quando alguma operação autorizada é realizada ou resolver casos menores ou
degenerados para entender qual é a lógica do problema. As soluções sempre usam
métodos algébricos, geométricos ou apenas a Lógica, mas essas estratégias são
importantes para se saber qual rumo tomar para resolver certos problemas e eu
gostaria de compartilhá-las aqui.
Vou citar alguns exemplos ilustrativos.
1. Invariantes
Uma das principais estratégias para resolução de problemas de olimpíadas é a procura por invariantes. O fundamento do Princípio da Invariância é simples: busca pelo que se mantém constante quando uma operação permitida é realizada. Entre as principais formas de invariantes destacam-se três, que serão apresentadas a seguir através de exemplos resolvidos.Exemplo 1:
Começando com o conjunto {3, 4, 12}, é permitido apagar dois números a e b e escrever em seus lugares (0,6.a – 0,8.b) e (0,8.a + 0,6.b). É possível chegar ao conjunto {4, 6, 12}?
Resolução: Repare que ${(0,6a – 0,8b)}^{2} + {(0,8a + 0,6b)}^{2} = a^2 + b^2$ , implicando que a soma dos quadrados dos números dos conjuntos obtidos é invariante. Como ${3}^{2} + {4}^{2} + {12}^{2} = {13}^{2}$ e ${4}^{2} + {6}^{2} + {12}^{2} = {14}^{2}$ então não é possível chegar ao conjunto ${4, 6, 12}$.
Exemplo 2:
Em cada um dos 10 degraus de uma escada existe uma rã. Cada rã pode, de um
pulo, colocar-se em outro degrau, mas quando uma rã faz isso, ao mesmo tempo,
uma outra rã pulará a mesma quantidade de degraus em sentido contrário: uma
sobe e outra desce. Conseguirão as rãs colocar-se todas juntas num mesmo degrau?
Resolução: Numeremos os degraus de
Fonte: Revista
Eureka!
2. Elementos extremos
Considere uma fileira de estudantes ordenada em forma decrescente segundo a
altura. A maioria deles tem dois vizinhos. Dois "elementos extremos",
o mais alto e o mais baixo, tem somente um vizinho, porém estes dois elementos
extremos possuem outras propriedades muito úteis. Por exemplo, quando contamos
os estudantes na fileira, a melhor maneira é começar com um destes elementos
extremos. Em matemática, algumas vezes trabalhamos com conjuntos cujos
elementos parecem ser equivalentes e cujas propriedades conhecidas são poucas.
Uma estratégia poderosíssima em tais casos é considerar o elemento, ou os
elementos, que de alguma forma são elementos extremos. Por exemplo, quando
consideramos um conjunto infinito de números naturais, o elemento extremo é seu
elemento menor. Para um conjunto finito de números reais os elementos extremos
são o máximo e o mínimo do conjunto.
Em muitos casos o elemento extremo é atrativo devido a que suas propriedades
adicionais nos permitem obter concluir sobre o mesmo elemento, ou sobre o do
conjunto como um todo. Por exemplo, em um triângulo o lado maior se opõe ao
ângulo maior e vice-versa.
Fonte: Revista
Eureka!
Exemplo 1:
Encontre rapidamente a soma dos números inteiros e positivos de
Considerando-se os elementos extremos, podemos observar que 1+100 = 2+99 =
3+98=… = 50+51.
Como a ordem das parcelas não altera a soma e existem 50 parcelas iguais a 101, basta fazer $101 \times 50 = 5050$, que é a resposta procurada.
Exemplo 2:
Carlinhos pensa num número ímpar positivo menor do que 10. Pedrinho se
dispõe a descobrir que número é esse fazendo a seguinte pergunta, quantas vezes
forem necessárias: “O número que você pensou é maior, menor ou igual a x
? ”. Note que x é um número que Pedrinho escolhe.
Quantas perguntas desse tipo Pedrinho poderá ter que fazer até descobrir o
número pensado por Carlinhos?
Suponha que o número seja 9 e considere, sem perda de generalidade, o número
5, que é a metade de
Daí, você saberá que o número escolhido é maior que 5. Agora considere o
número 8, que é 5 acrescentado ao maior inteiro maior que 2,5, que é a metade
de
Com a terceira pergunta, Pedrinho descobre o número escolhido.
Em geral, se Carlinhos pensa num número ímpar positivo menor do que n, então sendo 2^{m} a maior potência de 2 menor que n, o número de perguntas necessárias para descobrir o número é m. Por exemplo, se Carlinhos pensa num número ímpar positivo menor do que 1000, serão necessárias 9 perguntas, pois ${2}^{9} = 512 <1000$.
3. Casos menores
Exemplo 1:
(OBM 2004) Dizemos que um número natural é composto quando pode ser escrito como produto de dois números naturais maiores que 1. Assim, por exemplo, 91 é composto porque podemos escrever $91 = 7 \times 13$. Mostre que o número
$\displaystyle 2^{\left(2^{2004} + 2\right)} + 1$
é composto.
Vamos considerar os último algarismos das primeiras potências de 2. As primeiras potências de 2 são os números 2, 4, 8, 16, 32, 64, 128, 256, 512… Veja que os últimos algarismos se repetem nesse ciclo: 2, 4, 8, 6, 2…
Se n é múltiplo de 4, então, ${2}^{n}$ termina em $6$. Se $n$ deixa resto $2$ ao ser dividido por $4$, então ${2}^{n}$ termina em $4$. Como $2004 = 501 \times 4$, o último algarismo de $2^{2004}$ é $6$ e como $2^{2004}$ é múltiplo de $4$, o número $2^{\left(2^{2004} + 2\right)}$ termina em $4$ e $2^{\left(2^{2004} + 2\right)} + 1$ termina em $5$. Qualquer número que termina em $5$ é múltiplo de $5$ e, portanto, é composto.
Exemplo 2:
A resposta é $2^{n} - 1$.
Por exemplo, tomando $n = 2$ circunferências, temos o seguinte esquema:
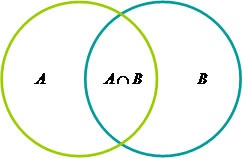
Observe que temos 3 regiões não interceptadas. Podemos intuir que cada
sub-região é uma intersecção de pelo menos duas das circunferências. O total de
possibilidades é a soma de todas as intersecções possíveis, (a soma das
combinações de n elementos tomados de
$\displaystyle \sum_{k=1}^n{n \choose k}$
Pelo Teorema da soma de uma linha do Triângulo de Pascal temos que $\displaystyle \sum_{k=0}^n{n \choose k} = 2^n$
Como $\displaystyle {n \choose 0} = 1$, temos que o número de intersecções possíveis é $2^n - 1$
Por exemplo, para $n = 3$ circunferências temos $2^3 - 1 = 7$ intersecções. De fato:

Há outra forma de se chegar a este resultado, por recorrência. Seja $A_{n}$ o número de regiões distintas e não subdivididas formadas pelas intersecções de n circunferências. Cada nova circunferência intercepta cada uma dessas regiões, dobrando o seu número e acrescenta uma nova região, que não é interceptada. Portanto, $A_{n+1} = 2A_{n} + 1$.
Resolvendo-se essa recorrência, obtemos $A_{n} = 2^{n} - 1$.
De fato:
$A_{n + 1} = 2A_{n} + 1 = 2(2^{n} - 1) + 1 = 2^{n + 1} - 2 + 1 = 2^{n + 1} - 1$.
Veja como seriam todas as possibilidades de intersecções para $n = 4$. Neste caso temos que o número máximo de intersecções é $2^4 - 1 = 15$ intersecções. Aqui elas assumem a forma elíptica, mas devemos lembrar que a circunferência é um caso particular de elipse.
A elipse tem 2 focos, que no caso da circunferência são sobrepostos.

4. Problemas correlatos
Exemplo 1:
Prove que não existe uma potência inteira de 2 que seja o resultado de uma reordenação dos algarismos de outra potência de 2?
Considerando que zeros à esquerda não contam, uma potência de 2 pode ser multiplicada por 2 ou 4 ou, no máximo, 8 para formar outra potência de 2 com a mesma quantidade de algarismos.
Um número da forma $10^{n}$ ao ser multiplicado por um número maior que 10 resulta em um número com um algarismo a mais. Logo, uma potência de 2 pode ser multiplicada por, no máximo, 8 para ter outra potência de 2 com a mesma quantidade de algarismos.
Um número formado pela reordenação dos algarismos de outro deixa o mesmo resto que o primeiro na divisão por 9.
Considerando-se um número n, temos que 2n ou 4n ou 8n não deixam o mesmo
resto que n na divisão por 9. Isso é possível verificar analisando-se cada um
dos possíveis restos da divisão de algum número por 9 (os algarismos de
Vamos considerar outra situação que envolve a soma dos algarismos de um número inteiro e positivo. Essa soma sempre deixa o mesmo resto na divisão por 9 que o próprio número. Por exemplo, 512 deixa resto 8 na divisão por 9 e a soma dos seus algarismos é 5 + 1 + 2 = 8.
Considerando que zeros à esquerda não contam, uma potência de 2 pode ser multiplicada por 2 ou 4 ou, no máximo, 8 para formar outra potência de 2 com a mesma quantidade de algarismos.
Um número da forma ${10}^{n}$ ao ser multiplicado por um número maior que 10 resulta em um número com um algarismo a mais. Logo, uma potência de 2 pode ser multiplicada por, no máximo, 8 para ter outra potência de 2 com a mesma quantidade de algarismos.
Um número formado pela reordenação dos algarismos de outro deixa o mesmo resto que o primeiro na divisão por 9.
Considerando-se um número n, temos que $2n$ ou $4n$ ou $8n$ não deixam o mesmo
resto que n na divisão por 9. Isso é possível verificar analisando-se cada um
dos possíveis restos da divisão de algum número por 9 (os algarismos de
Exemplo 2:
Encontre todas as sequências de números inteiros, positivos consecutivos cujas somas dos seus termos seja igual a 100.
Vamos considerar outra situação que envolve a soma dos termos de sequências de números. A fórmula da soma dos termos de uma progressão aritmética é
$S_n = \displaystyle \frac{({a}_{1} + {a}_{n})n}{2}$
Então, como $a_n = a_1 + (n - 1)r$ e como os números são consecutivos, temos que $r=1$.
Então $a_n = a_1 + (n - 1)$. Substituindo-se isso em $\frac{({a}_{1} + {a}_{n})n}{2}$ e igualando a $100$, temos que:
$(2{a}_{1} + n - 1)n = 200$
$\displaystyle n = \frac{200}{(2{a}_{1} + n - 1)}$
Como $n$ e $(2{a}_{1} + n - 1)$ devem ser um números inteiros e positivos, então $n$ deve ser um divisor inteiro de $200$. Os divisores de $200$ são $d_{1} = 1$, $d_{2} = 2$, $d_{3} = 4$, $d_{4} = 5$, $d_{5} = 8$, $d_{6} = 10$, $d_{7} = 20$, $d_{8} = 25$, $d_{9} = 40$, $d_{1} = 50$, $d_{11} = 100$ e $d_{12} = 200$.
Sendo $1 \leq k \leq 12$, temos que:
$\displaystyle a_1 = \frac{\frac{200}{d_k} + 1 - n}{2}$
$\displaystyle a_1 = \frac{\frac{200}{d_k} + 1 - {d}_{k}}{2}$
Igualando-se $\frac{\frac{200}{{d}_{k}} + 1 - {d}_{k}}{2}$ a cada um dos divisores de $200$, obtemos os possíveis valores de $a_1$ e, caso sejam inteiros e positivos encontramos as sequências procuradas, que são estas:
Por exemplo, se $n=1$, então $(2{a}_{1} + {d}_{1} - 1) = \frac{200}{1} = 200$.
$(2{a}_{1} + {d}_{1} - 1) = 200$
$(2{a}_{1} + 1 - 1) = 200$
$\displaystyle \boxed{a_1 = 100}$
Se $n = 1$, então $a_1 = 100$ e a sequência é $(100)$.
Se $n = 5$, então $a_1 = 18$ e a sequência é $(18, 19, 20, 21, 22)$.
Se $n = 8$, então $a_1 = 9$ e a sequência é $(9, 10, 11, 12, 13, 14, 15, 16)$.
Existem muitas outras estratégias desse tipo, mas as principais que eu conheço são essas.
Comentários
Postar um comentário